Learned Systems
CSAIL Logo
DSAIL Logo

LSI: A Learned Secondary Index Structure

Authors: Dominik Horn, Andreas Kipf, Pascal Pfeil

We are happy to present LSI: A Learned Secondary Index Structure and our accompanying open-source C++ implementation that can easily be included in other projects using CMake FetchContent. LSI is a learned secondary index. It offers competitive lookup performance on real-world datasets while reducing space usage by up to 6x compared to state-of-the-art secondary index structures.

Motivation

Most learned index structures focus on primary indexing where base data is stored in sorted order. Since a table can only be sorted by a single key, it is therefore of high interest to study the feasibility of applying learned techniques to indexing unsorted, secondary columns. Specifically, we were aiming to come up with an off-the-shelf usable index structure that manages to retain the proven benefits of learned primary indexes as best as possible.

LSI Overview

LSI consists of two parts. A pre-existing learned index structure acting as an approximate index, e.g., a PLEX, and a permutation vector. The learned index is trained over a temporary sorted copy of the base data’s keys. The permutation vector retains a mapping from the sorted key’s positions to offsets (tuple IDs) into the base data. The following paragraph contains a schematic illustration of LSI. A more detailed explanation, especially concerning how we achieved LSI’s space efficiency, can be found in our paper.

Lookups

Querying LSI works in three steps, as illustrated below:

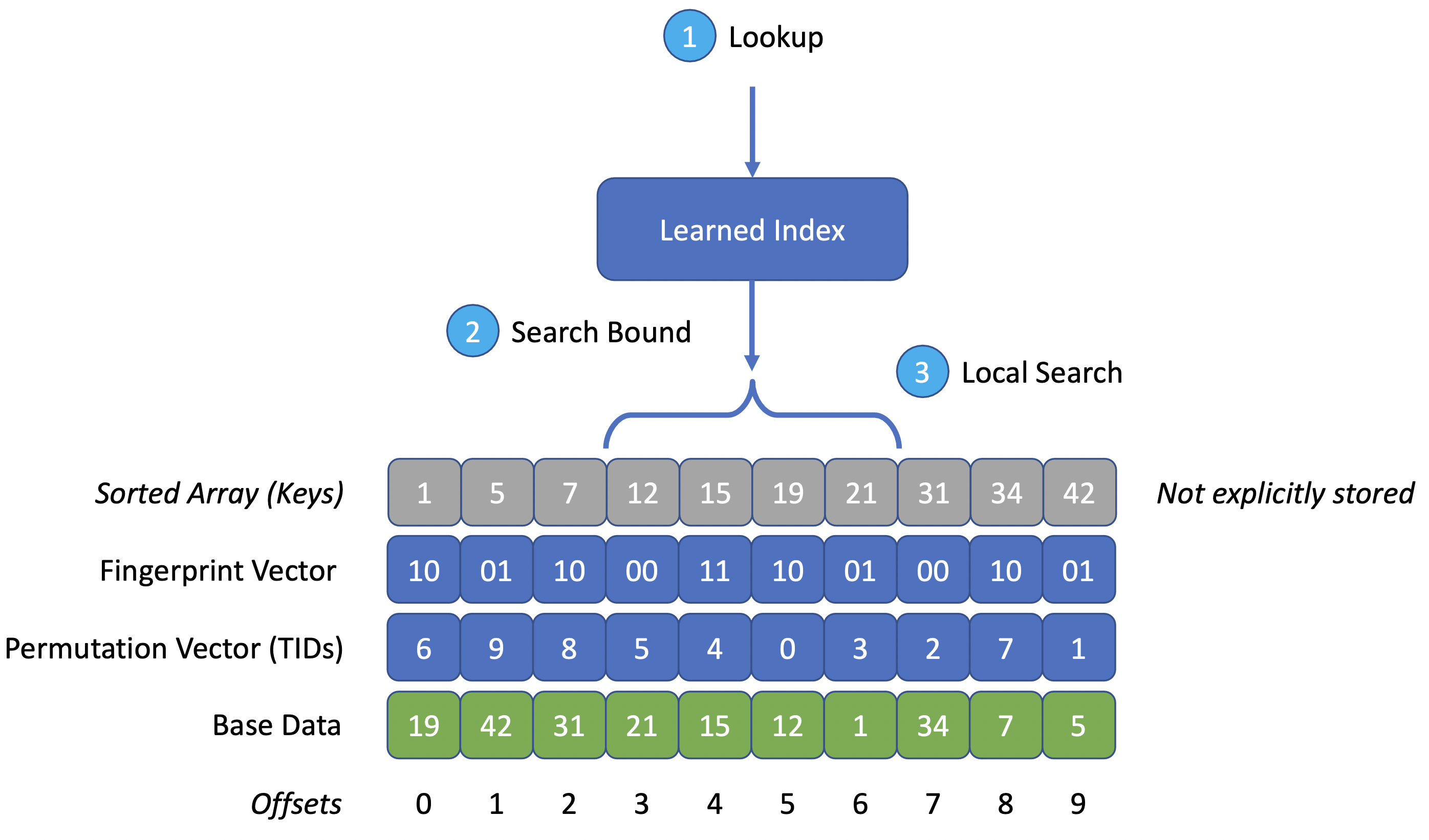
LSI Architecture Overview

  1. Query the learned index for an approximate position in the sorted base data. Again, note that the sorted representation is not actually stored and only exists temporarily during construction.
  2. Obtain search bounds based on the approximate position and the learned index’s error bounds. These can either be guaranteed by construction, as is the case with PLEX, or could be measured and retained during training.
  3. Conduct a local search over the permutation vector to locate the key.
    • Lower-Bound Lookups perform a binary search. Note that this requires O(log k) probes into the base data for a search interval of size k. This could potentially be prohibitively costly in practice, e.g., when base data is not fully loaded into main memory.
    • Equality Lookups can be sped up by retaining fingerprint bits for each key and performing a linear scan over the search interval. This requires O(k) base data probes for a search interval of size k. However, each additional fingerprint bit roughly halves the number of required accesses.

Evaluation

Evaluations were conducted on a c5.9xlarge AWS machine with 36 vCPUs and 72 GiB of RAM using four real-world datasets from SOSD, each with 200 million 64-bit unsigned integer keys:

All experiments ran single threaded. To prevent skew from potential out-of-order execution, we insert a full memory fence using the compiler’s built in __sync_synchronize() after each lookup. A more detailed writeup of our findings can be found in our paper.

Lower-Bound Lookups

To benchmark lower-bound lookups, we randomly remove 10% of the elements from the datasets before building each index. We only query for non-keys. LSI with PLEX as its approximate index is competitive with ART’s latency, while consuming up to 6x less space. It is twice as fast as BTree while reducing space consumption by up to 3x.

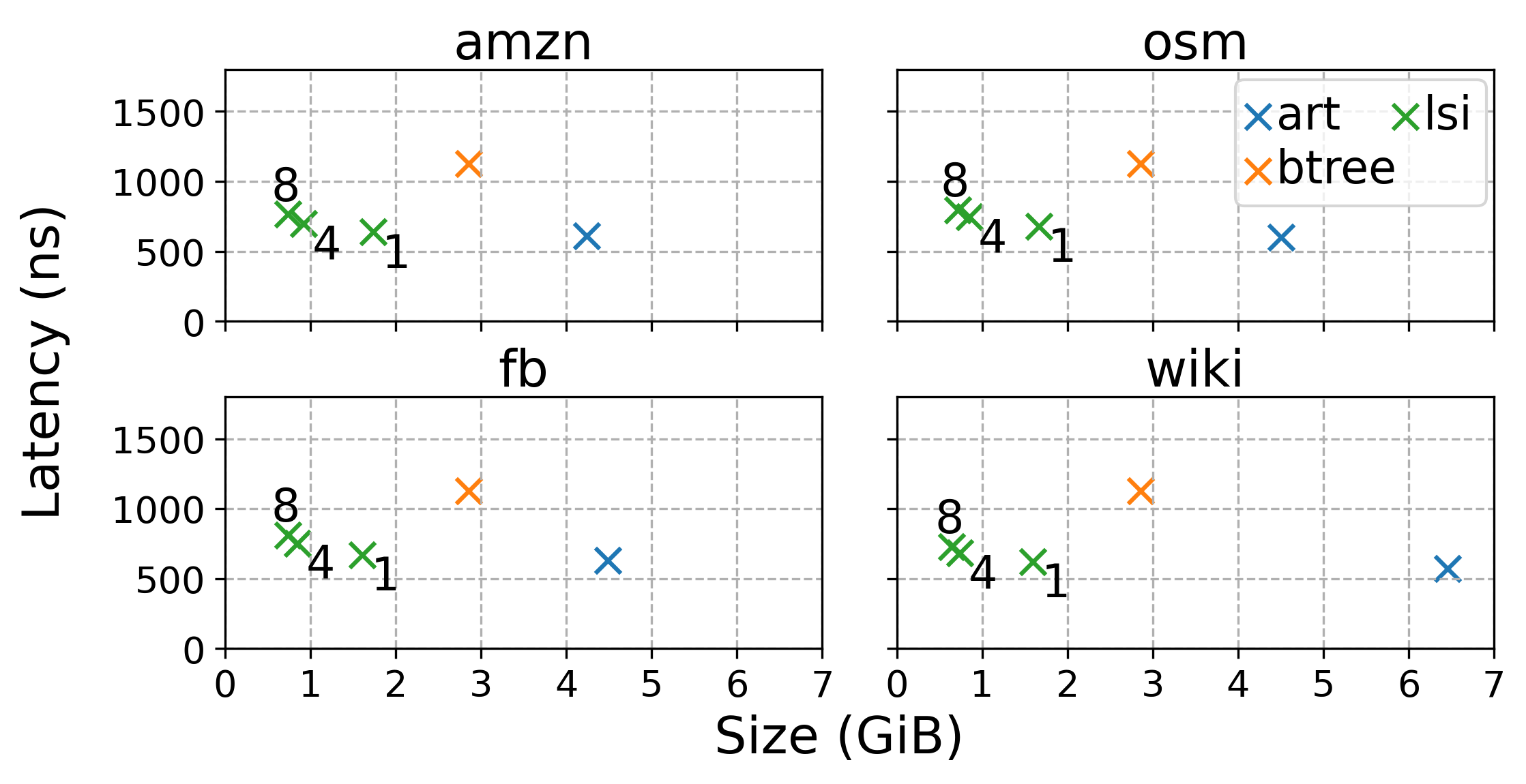
lowerbounds benchmark on all four datasets

Note that BTree was constructed by first sorting the data and bulk loading it afterwards. This enables denser nodes and therefore faster lookups. Inserting keys in random order one after another increased space usage by roughly 33% and slowed down lookups by more than 20%. The text annotations denote the LSI model’s error bound.

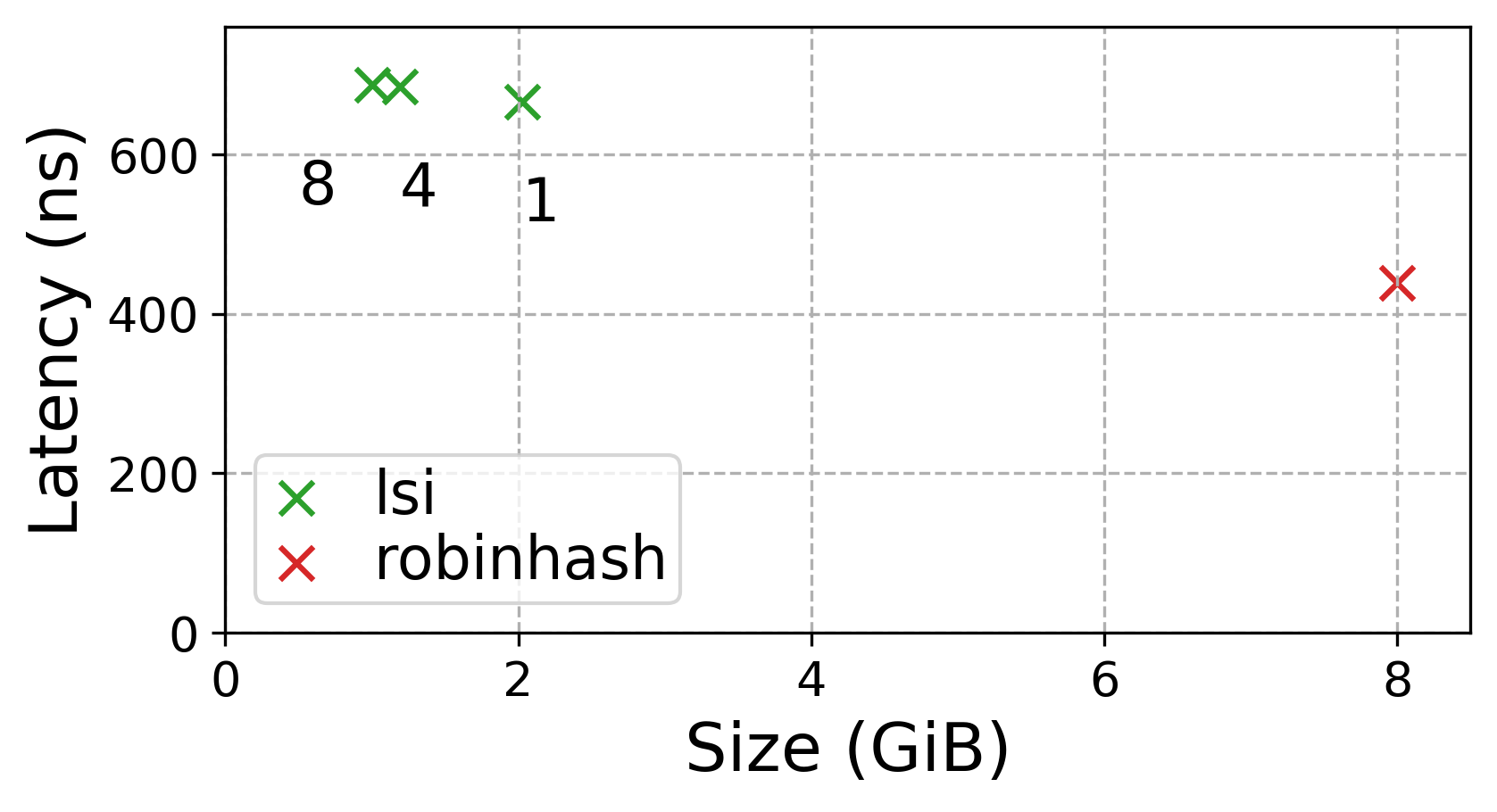
Equality Lookups

Although LSI with PLEX as its approximate index is around 1.5x slower than the robin-hood hash table implementation RobinMap, it consumes less than a quarter of the space. The text annotations again denote the LSI model’s error bound. Note that we used the amzn dataset for this test, only to later discover that RobinMap’s hash function appears to be unfavorably biased in this case. On fb and osm, RobinMap’s lookup only takes 340ns compared to the 440ns on amzn. Space consumption does not change.

equality benchmark on amzn

Build Time

We measured the true end-to-end build time for each index given an unsorted continuous in-memory representation of each dataset’s 200 million keys. LSI is competitive in terms of build time. It performs slightly worse than BTree, but surpasses ART on every dataset we tested. As expected, tighter error bounds on the approximate index increase build time.

BTree is constructed by first sorting and the bulk loading all keys. This is about 8x faster than inserting keys in unsorted order one by one. ART does not have a bulk-loading interface, however, its construction time is still cut in half when keys are first sorted and then inserted one after another. We suspect this effect is primarily caused by better cache behavior during construction.

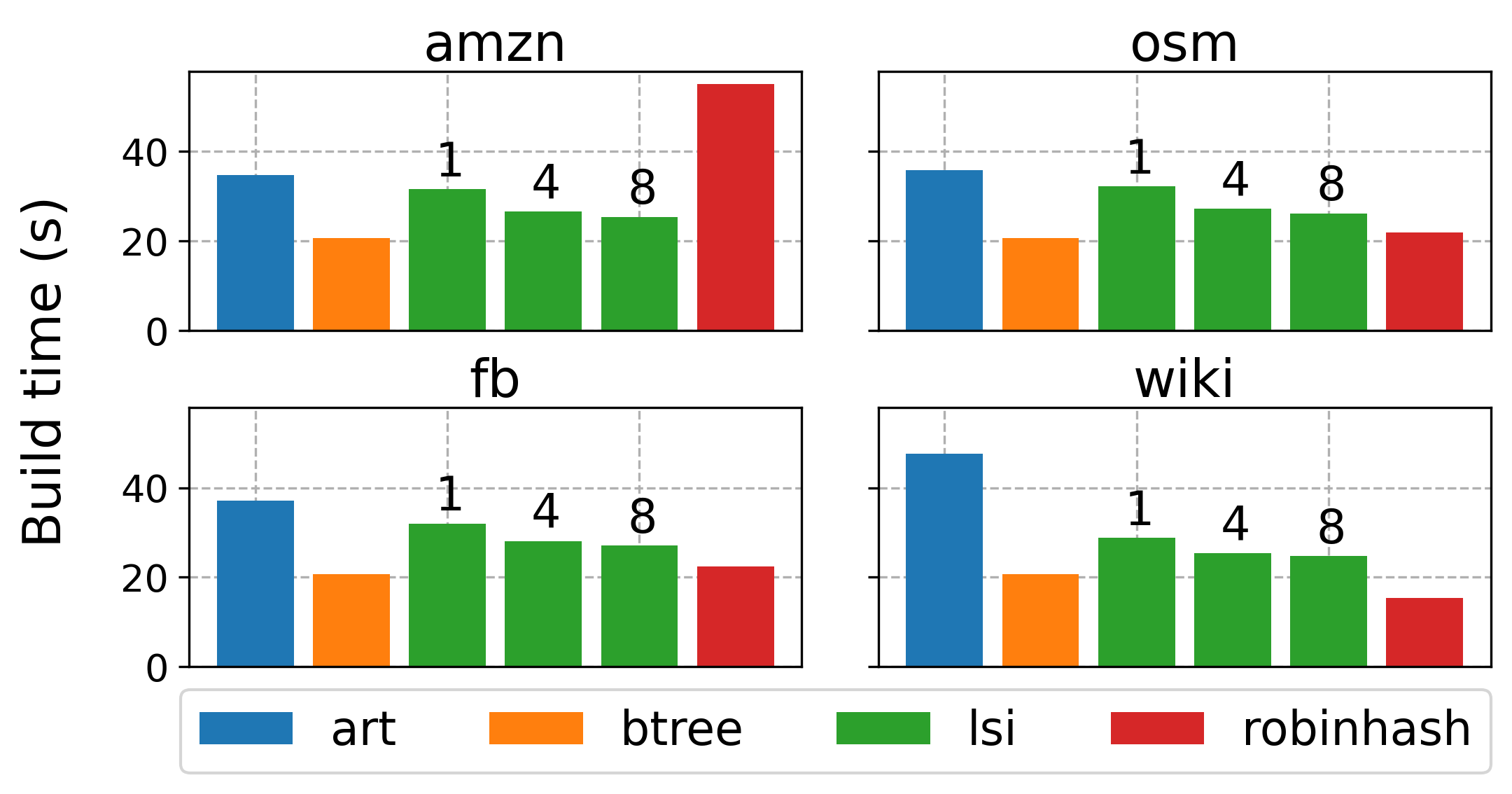
build time comparison on all four datasets

Note that we would have expected RobinMap to exhibit equal build throughput on amzn, fb and osm. Further investigation is required to determine why it performs so poorly on amzn. We suspect that the hash function, which we have no control over, might be unfavorably biased in this case. More than half of all elements from wiki are duplicates. For this reason, build times for RobinMap on this dataset appear faster.

Fingerprint Configuration

We conducted a micro experiment to study the trade off between binary search and linear search with fingerprints. For this purpose, we trained LSI with PLEX as an approximate index on amzn using various errors and fingerprint bit sizes (denoted in brackets), and compared lookup latencies:

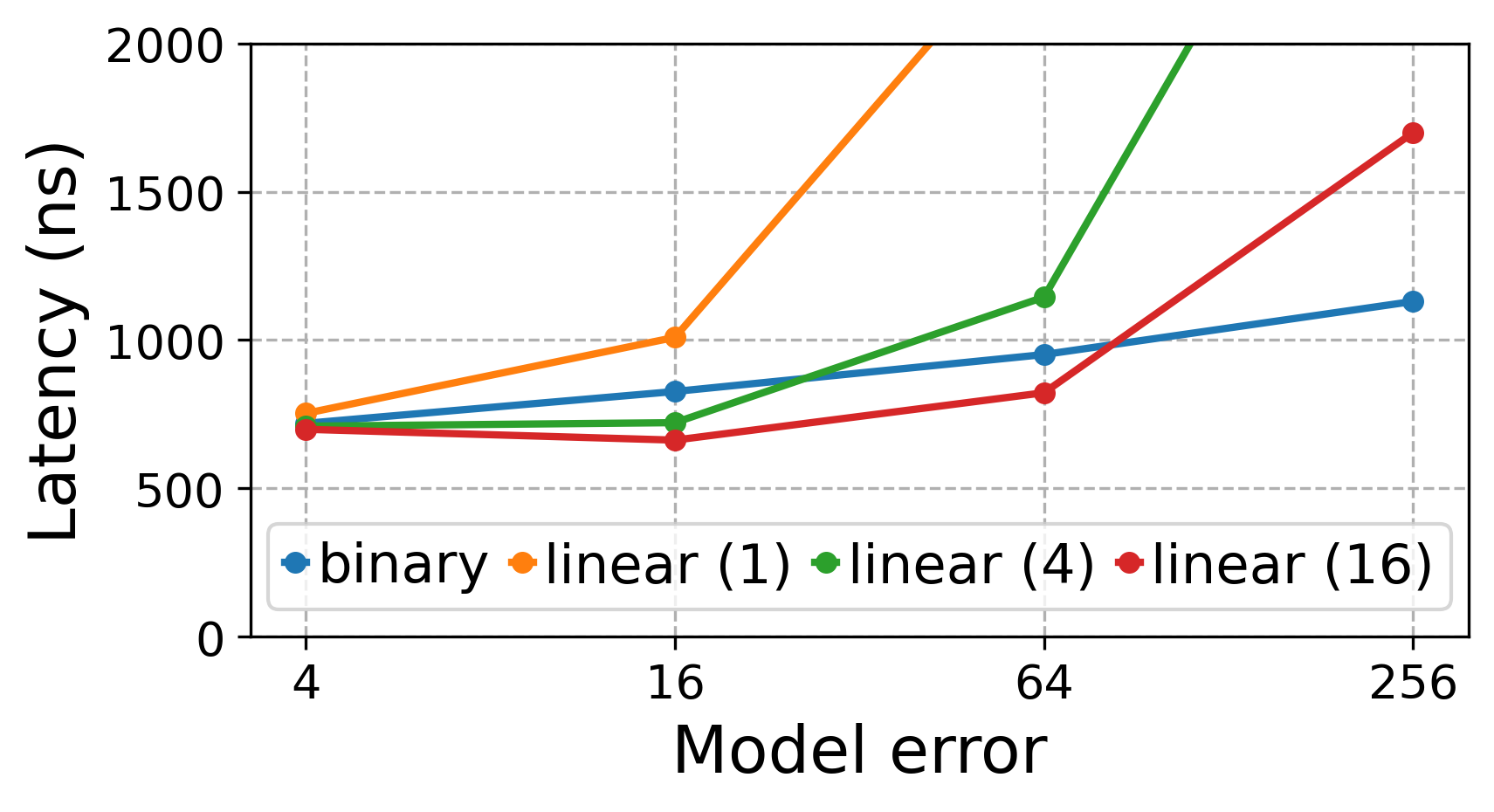
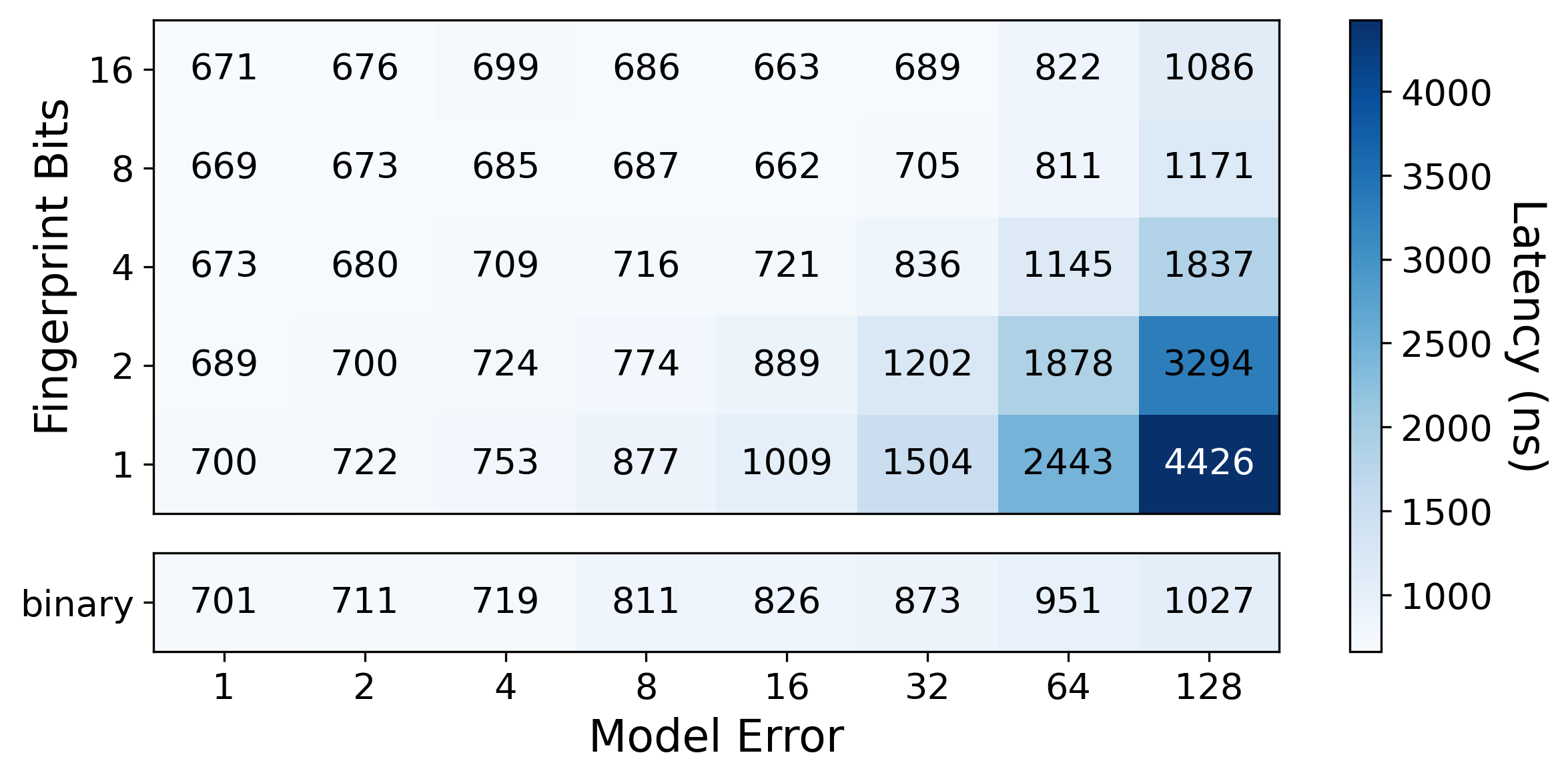
micro experiment as line plot micro experiment as heat map

For a search bound of size k, binary search always performs O(log k) probes into the base data, while linear search requires O(k). Each additional fingerprint bit will roughly halve the number of base data accesses.

Future Work

We are excited about our promising first results of approaching secondary indexing using learned techniques. For production readiness, we will need to add support for inserts. This will require two main adjustments. First, the approximate index has to be updateable. We could either attempt to extend PLEX with support for inserts, or use an existing off-the-shelf model that supports inserts like PGM. Additionally, we will have to find a better way to deal with dynamic updates to the permutation vector. As implemented currently, each update will require shifting and incrementing values, or O(n) time.

Another interesting direction is to try and reduce base data accesses during lower-bound lookups. While we could just store a copy of all keys in the permutation vector, similar to BTree’s leaf layer, this will negate most of LSI’s space savings. However, there might be an opportunity to store just enough information to reconstruct enough information about the keys to enable efficient (binary) searching. Stay tuned!